import numpy as np
from sklearn import datasets
from matplotlib import pyplot as pltPreface
In this post, we will explore a simple version of the spectral clustering algorithm for clustering data points. Spectral clustering is an important tool for identifying meaningful parts of data sets with complex structure.
Notation
In all the math below:
- Boldface capital letters like \(\mathbf{A}\) refer to matrices (2d arrays of numbers).
- Boldface lowercase letters like \(\mathbf{v}\) refer to vectors (1d arrays of numbers).
- \(\mathbf{A}\mathbf{B}\) refers to a matrix-matrix product (
A@B). \(\mathbf{A}\mathbf{v}\) refers to a matrix-vector product (A@v).
Introduction
To begin, let’s look at an example where we don’t need spectral clustering.
n = 200
np.random.seed(1111)
X, y = datasets.make_blobs(n_samples=n, shuffle=True, random_state=None, centers = 2, cluster_std = 2.0)
plt.scatter(X[:,0], X[:,1])<matplotlib.collections.PathCollection at 0x7faef6120400>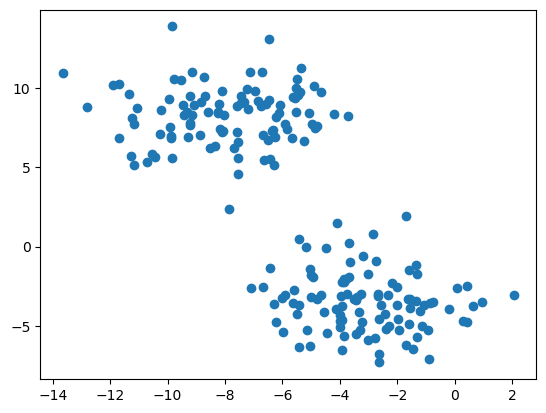
Clustering refers to the task of separating this data set into the two natural “blobs.” K-means is a very common way to achieve this task, which has good performance on circular-ish blobs like these:
from sklearn.cluster import KMeans
km = KMeans(n_clusters = 2)
km.fit(X)
plt.scatter(X[:,0], X[:,1], c = km.predict(X))<matplotlib.collections.PathCollection at 0x7faef66cda00>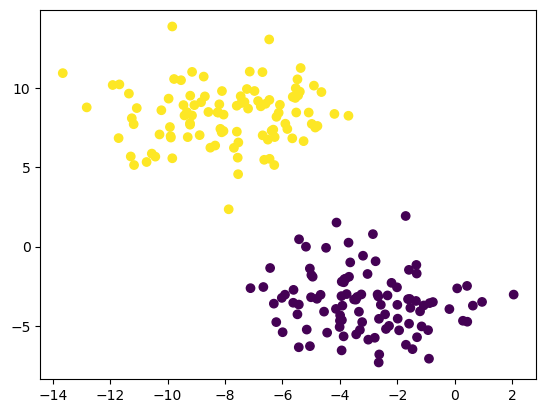
Harder Clustering
That was all well and good, but what if our data is “shaped weird”?
np.random.seed(1234)
n = 200
X, y = datasets.make_moons(n_samples=n, shuffle=True, noise=0.05, random_state=None)
plt.scatter(X[:,0], X[:,1])<matplotlib.collections.PathCollection at 0x7faef6837eb0>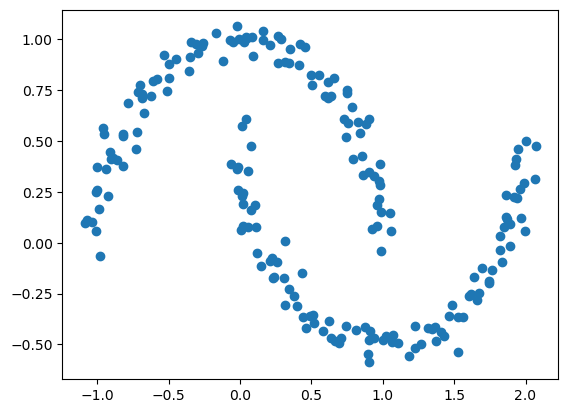
We can still make out two meaningful clusters in the data, but now they aren’t blobs but crescents. As before, the Euclidean coordinates of the data points are contained in the matrix X, while the labels of each point are contained in y. Now k-means won’t work so well, because k-means is, by design, looking for circular clusters.
km = KMeans(n_clusters = 2)
km.fit(X)
plt.scatter(X[:,0], X[:,1], c = km.predict(X))<matplotlib.collections.PathCollection at 0x7faef6a80c40>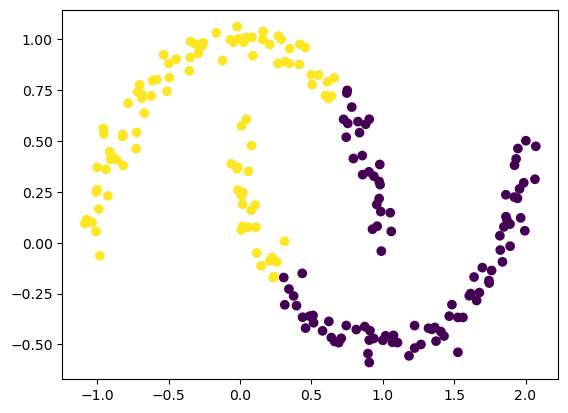
Whoops! That’s not right!
As we’ll see, spectral clustering is able to correctly cluster the two crescents. In the following parts, we will derive and implement spectral clustering.
Part A
In this part, we will construct the similarity matrix \(\mathbf{A}\). \(\mathbf{A}\) should be a matrix (2d np.ndarray) with shape (n, n) (recall that n is the number of data points).
When constructing the similarity matrix, we will use a parameter epsilon. Entry A[i,j] should be equal to 1 if X[i] (the coordinates of data point i) is within distance epsilon of X[j] (the coordinates of data point j), and 0 otherwise.
For this matrix, the diagonal entries A[i,i] should all be equal to zero. We will use epsilon = 0.4 for now.
from sklearn.metrics import pairwise_distances
def construct_similarity_matrix(X, epsilon):
"""
Constructs the similarity matrix
Args:
X: original matrix containing coordinates for all data points
epsilon: the benchmark distance for classifying 'similarity'
Return:
similarity_matrix: a n by n similarity matrix
"""
distances = pairwise_distances(X)
similarity_matrix = np.where(distances <= epsilon, 1, 0)
np.fill_diagonal(similarity_matrix, 0) # diagonal entries are 0
return similarity_matrix
A = construct_similarity_matrix(X, 0.4)
Aarray([[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 1, 0],
...,
[0, 0, 0, ..., 0, 1, 1],
[0, 0, 1, ..., 1, 0, 1],
[0, 0, 0, ..., 1, 1, 0]])Part B
The matrix A now contains information about which points are near (within distance epsilon) which other points. We now pose the task of clustering the data points in X as the task of partitioning the rows and columns of A.
Let \(d_i = \sum_{j = 1}^n a_{ij}\) be the \(i\)th row-sum of \(\mathbf{A}\), which is also called the degree of \(i\). Let \(C_0\) and \(C_1\) be two clusters of the data points. We assume that every data point is in either \(C_0\) or \(C_1\). The cluster membership as being specified by y. We think of y[i] as being the label of point i. So, if y[i] = 1, then point i (and therefore row \(i\) of \(\mathbf{A}\)) is an element of cluster \(C_1\).
The binary norm cut objective of a matrix \(\mathbf{A}\) is the function
\[N_{\mathbf{A}}(C_0, C_1)\equiv \mathbf{cut}(C_0, C_1)\left(\frac{1}{\mathbf{vol}(C_0)} + \frac{1}{\mathbf{vol}(C_1)}\right)\;.\]
In this expression,
- \(\mathbf{cut}(C_0, C_1) \equiv \sum_{i \in C_0, j \in C_1} a_{ij}\) is the cut of the clusters \(C_0\) and \(C_1\).
- \(\mathbf{vol}(C_0) \equiv \sum_{i \in C_0}d_i\), where \(d_i = \sum_{j = 1}^n a_{ij}\) is the degree of row \(i\) (the total number of all other rows related to row \(i\) through \(A\)). The volume of cluster \(C_0\) is a measure of the size of the cluster.
A pair of clusters \(C_0\) and \(C_1\) is considered to be a “good” partition of the data when \(N_{\mathbf{A}}(C_0, C_1)\) is small. To see why, let’s look at each of the two factors in this objective function separately.
B.1 The Cut Term
First, the cut term \(\mathbf{cut}(C_0, C_1)\) is the number of nonzero entries in \(\mathbf{A}\) that relate points in cluster \(C_0\) to points in cluster \(C_1\). Saying that this term should be small is the same as saying that points in \(C_0\) shouldn’t usually be very close to points in \(C_1\).
Here, we will write a function called cut(A,y) to compute the cut term.
def cut(A, y):
"""
Computes the cut term
Args:
A: a similarity matrix
y: the labels for the clusters
Return:
cut_value: the cut term
"""
n = A.shape[0]
cut_value = 0
for i in range(n):
for j in range(n):
if y[i] != y[j]: # these are in different clusters
cut_value += A[i, j]
return cut_value/2 # avoid double-countingNow, we will compute the cut objective for the true clusters y. Then, we will generate a random vector of random labels of length n, with each label equal to either 0 or 1, and check the cut objective for the random labels. We should get that the cut objective for the true labels is much smaller than the cut objective for the random labels.
cut_true = cut(A, y)
np.random.seed(42)
y_random = np.random.randint(0, 2, size=n) # random labels
cut_random = cut(A, y_random)
print(cut_true)
print(cut_random)13.0
1147.0This shows that this part of the cut objective indeed favors the true clusters over the random ones.
B.2 The Volume Term
Now, the volume term. As mentioned above, the volume of cluster \(C_0\) is a measure of how “big” cluster \(C_0\) is. If we choose cluster \(C_0\) to be small, then \(\mathbf{vol}(C_0)\) will be small and \(\frac{1}{\mathbf{vol}(C_0)}\) will be large, leading to an undesirable higher objective value.
Synthesizing, the binary normcut objective asks us to find clusters \(C_0\) and \(C_1\) such that:
- There are relatively few entries of \(\mathbf{A}\) that join \(C_0\) and \(C_1\).
- Neither \(C_0\) and \(C_1\) are too small.
We will write a function called vols(A,y) which computes the volumes of \(C_0\) and \(C_1\), returning them as a tuple. For example, v0, v1 = vols(A,y) should result in v0 holding the volume of cluster 0 and v1 holding the volume of cluster 1. Then, we will write a function called normcut(A,y) which uses cut(A,y) and vols(A,y) to compute the binary normalized cut objective of a matrix A with clustering vector y.
def vols(A, y):
"""
Computes the volume term
Args:
A: a similarity matrix
y: the labels for the clusters
Return:
v0, v1: the volumes of cluster 0 and cluster 1
"""
v0 = np.sum(A[np.where(y == 0)]) # volume of cluster 0
v1 = np.sum(A[np.where(y == 1)]) # volume of cluster 1
return v0, v1
def normcut(A, y):
"""
Computes the binary norm cut objective
Args:
A: a similarity matrix
y: the labels for the clusters
Return:
normcut_value: the binary norm cut objective
"""
cut_value = cut(A, y)
v0, v1 = vols(A, y)
normcut_value = cut_value * (1 / v0 + 1 / v1)
return normcut_valueNow, we will compare the normcut objective using both the true labels y and the fake labels we generated above.
print(normcut(A,y))
print(normcut(A,y_random))0.011518412331615225
1.0159594530373053We notice that the normcut for the true labels is significantly smaller than the normcut for the fake labels.
Part C
We have now defined a normalized cut objective which takes small values when the input clusters are (a) joined by relatively few entries in \(A\) and (b) not too small. One approach to clustering is to try to find a cluster vector y such that normcut(A,y) is small. However, this is an NP-hard combinatorial optimization problem, which means that may not be possible to find the best clustering in practical time, even for relatively small data sets. We need a math trick!
Here’s the trick: define a new vector \(\mathbf{z} \in \mathbb{R}^n\) such that:
\[ z_i = \begin{cases} \frac{1}{\mathbf{vol}(C_0)} &\quad \text{if } y_i = 0 \\ -\frac{1}{\mathbf{vol}(C_1)} &\quad \text{if } y_i = 1 \\ \end{cases} \]
Note that the signs of the elements of \(\mathbf{z}\) contain all the information from \(\mathbf{y}\): if \(i\) is in cluster \(C_0\), then \(y_i = 0\) and \(z_i > 0\).
Next, by linear algebra, we can show that
\[\mathbf{N}_{\mathbf{A}}(C_0, C_1) = \frac{\mathbf{z}^T (\mathbf{D} - \mathbf{A})\mathbf{z}}{\mathbf{z}^T\mathbf{D}\mathbf{z}}\;,\]
where \(\mathbf{D}\) is the diagonal matrix with nonzero entries \(d_{ii} = d_i\), and where \(d_i = \sum_{j = 1}^n a_i\) is the degree (row-sum) from before.
Now, we will achieve three tasks in this part:
- We will write a function called
transform(A,y)to compute the appropriate \(\mathbf{z}\) vector givenAandy, using the formula above. - Then, we will check the equation above that relates the matrix product to the normcut objective, by computing each side separately and checking that they are equal.
- We will also check the identity \(\mathbf{z}^T\mathbf{D}\mathbb{1} = 0\), where \(\mathbb{1}\) is the vector of
nones (i.e.np.ones(n)). This identity effectively says that \(\mathbf{z}\) should contain roughly as many positive as negative entries.
The equation above is exact, but computer arithmetic is not! np.isclose(a,b) is a good way to check if a is “close” to b, in the sense that they differ by less than the smallest amount that the computer is (by default) able to quantify.
def transform(A, y):
"""
Transforms into the z vector
Args:
A: a similarity matrix
y: the labels for the clusters
Return:
z: a new z vector
"""
v0, v1 = vols(A, y)
z = np.zeros_like(y, dtype=np.float32)
z[y == 0] = 1 / v0
z[y == 1] = -1 / v1
return zD = np.diag(np.sum(A, axis=1)) # by definition
def check_normcut(A, y):
"""
Checks for equality of normcut objective to the matrix product
Args:
A: a similarity matrix
y: the labels for the clusters
Return:
True if equal, False otherwise
"""
z = transform(A, y)
num = z.T @ (D - A) @ z
denom = z.T @ D @ z
mat_result = num / denom
return np.isclose(mat_result, normcut(A,y))
check_normcut(A, y)Truedef check_identity(A, y):
"""
Checks that z contains as many positive as negative entries
Args:
A: a similarity matrix
y: the labels for the clusters
Return:
True if equal, False otherwise
"""
z = transform(A, y)
zD_ones = z.T @ D @ np.ones(n)
return np.isclose(zD_ones, 0, atol = 1e-7)
check_identity(A,y)TruePart D
In the last part, we saw that the problem of minimizing the normcut objective is mathematically related to the problem of minimizing the function
\[ R_\mathbf{A}(\mathbf{z})\equiv \frac{\mathbf{z}^T (\mathbf{D} - \mathbf{A})\mathbf{z}}{\mathbf{z}^T\mathbf{D}\mathbf{z}} \]
subject to the condition \(\mathbf{z}^T\mathbf{D}\mathbb{1} = 0\). It’s actually possible to bake this condition into the optimization, by substituting for \(\mathbf{z}\) the orthogonal complement of \(\mathbf{z}\) relative to \(\mathbf{D}\mathbf{1}\). In the code below, orth_obj function is defined, which handles this.
Next, we will use the minimize function from scipy.optimize to minimize the function orth_obj with respect to \(\mathbf{z}\). Note that this computation might take a little while. Explicit optimization can be pretty slow! We will give the minimizing vector a name z_min.
def orth(u, v):
return (u @ v) / (v @ v) * v
e = np.ones(n)
d = D @ e
def orth_obj(z):
z_o = z - orth(z, d)
return (z_o @ (D - A) @ z_o)/(z_o @ D @ z_o)from scipy.optimize import minimize
z = np.random.rand(n)
result = minimize(orth_obj, z)
z_min = result.x
z_minarray([ 33.56667894, 26.37316335, -21.39702164, -20.55071611,
-23.49521762, -22.22583467, -20.58454322, -20.56529733,
17.32151832, 12.92074237, 22.78649358, -21.6425766 ,
-3.93000947, 20.62219017, 30.48792501, 25.65359739,
19.53087355, -21.36003169, -24.4363914 , -22.78690083,
22.22146152, 10.64059859, 33.58854065, -20.60080751,
-26.02027458, 15.19921269, -20.69525676, 21.13293901,
18.95811059, -21.00525524, -20.68958909, 34.04993781,
25.19032729, 24.50867291, 18.27983536, 27.77539342,
-26.00158657, 33.13506718, 29.25427799, -22.3317278 ,
24.42996414, -21.21719816, -21.04328742, -25.90130481,
-25.78291401, -21.18474707, -21.30937214, 22.4242508 ,
30.07309516, 4.23764119, -21.26852308, -20.67189647,
33.57741684, 20.975337 , -26.22610425, -24.91284151,
27.89415393, 11.56344857, 33.17995203, -21.19698778,
-26.07863767, -24.07099584, 17.17040637, -21.31657182,
19.87883457, -22.43744228, -26.08559129, -25.75230516,
-21.37557797, 33.51214037, 28.39180555, 32.48717228,
33.55623108, -21.15625599, -25.56897992, -19.14888222,
14.92566763, -21.06860386, 33.22218498, -22.22972484,
-19.52092689, -23.70888334, -25.36223788, 23.17301992,
23.07437633, 29.08387663, 24.55973722, -21.17014922,
-21.52601955, -21.01648092, -20.87912299, 17.17576485,
-22.03067982, -21.27411166, 11.51371715, 12.93823407,
33.13294229, 28.90292165, -24.71950125, -20.66092009,
33.28195361, 30.07375766, 28.0527965 , -14.50319656,
24.82600383, 23.3097561 , -23.80433908, -20.75097155,
26.70245317, 20.45056606, -23.5815637 , -24.8964045 ,
-21.43036126, 25.8047085 , -21.15719993, -26.18143098,
-27.86492963, -20.53480694, 11.55026781, 25.45722698,
32.63447792, -23.05458713, 18.14553997, 31.47060664,
33.6672929 , -25.15117026, 27.62178804, -20.20282002,
33.97240791, 11.54809532, -25.58954778, -20.57088731,
-21.21076092, -21.04059505, 32.26086804, 33.3914734 ,
22.60475507, 21.19481961, 21.4986715 , 34.09257895,
14.08214772, 31.64437103, -25.63123855, -21.32475067,
33.7862901 , -25.52134551, -24.07395441, -24.72590513,
-20.9547022 , -21.29166206, -21.0474039 , -25.59786566,
-25.58351664, 15.18748075, 30.77139142, -26.05066909,
33.98671044, -20.66262663, -25.5539579 , -25.43757765,
26.4635911 , 28.12163816, -22.39866538, -21.17350504,
11.91792664, 15.23261131, 23.26120506, -21.3482099 ,
-20.5920695 , -20.57769699, 32.7390437 , -24.86264842,
20.4007099 , 22.4301347 , 29.0808605 , -21.3753384 ,
-21.07642789, -24.75473525, -20.63617456, 31.5161828 ,
19.54006394, -25.28257919, -24.04723688, 14.57176239,
17.28917035, 16.73722775, -21.79058334, 18.31688394,
27.92984478, 30.08404797, -21.33173509, 26.50436567,
-21.76764741, 31.85749159, 23.6364957 , 25.68592432,
15.57119198, -21.19872538, -20.63305669, -21.10856242])There’s a cheat going on here! We originally specified that the entries of \(\mathbf{z}\) should take only one of two values (back in Part C), whereas now we’re allowing the entries to have any value! This means that we are no longer exactly optimizing the normcut objective, but rather an approximation. This cheat is so common that deserves a name: it is called the continuous relaxation of the normcut problem.
Part E
Recall that, by design, only the sign of z_min[i] actually contains information about the cluster label of data point i. Thus, we plot the original data, using one color for points such that z_min[i] < 0 and another color for points such that z_min[i] >= 0.
import matplotlib.pyplot as plt
colors = ['red' if z < 0 else 'blue' for z in z_min]
plt.scatter(X[:, 0], X[:, 1], c=colors)
plt.title('Data Clustering')
plt.show()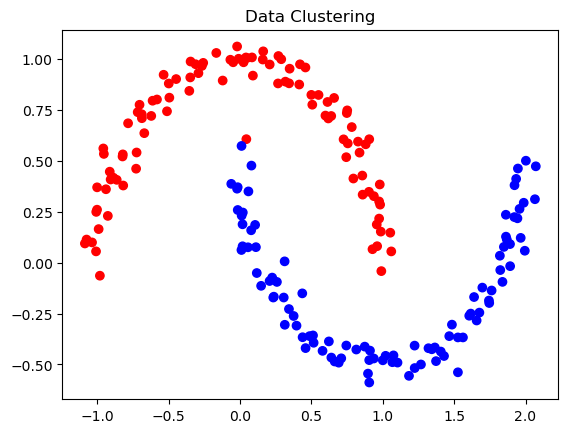
This looks great, but can we make the process quicker?
Part F
Explicitly optimizing the orthogonal objective is way too slow to be practical. If spectral clustering required that we do this each time, no one would use it.
The reason that spectral clustering actually matters, and indeed the reason that spectral clustering is called spectral clustering, is that we can actually solve the problem from Part E using eigenvalues and eigenvectors of matrices.
Recall that what we would like to do is minimize the function
\[ R_\mathbf{A}(\mathbf{z})\equiv \frac{\mathbf{z}^T (\mathbf{D} - \mathbf{A})\mathbf{z}}{\mathbf{z}^T\mathbf{D}\mathbf{z}} \]
with respect to \(\mathbf{z}\), subject to the condition \(\mathbf{z}^T\mathbf{D}\mathbb{1} = 0\).
The Rayleigh-Ritz Theorem states that the minimizing \(\mathbf{z}\) must be the solution with smallest eigenvalue of the generalized eigenvalue problem
\[ (\mathbf{D} - \mathbf{A}) \mathbf{z} = \lambda \mathbf{D}\mathbf{z}\;, \quad \mathbf{z}^T\mathbf{D}\mathbb{1} = 0\]
which is equivalent to the standard eigenvalue problem
\[ \mathbf{D}^{-1}(\mathbf{D} - \mathbf{A}) \mathbf{z} = \lambda \mathbf{z}\;, \quad \mathbf{z}^T\mathbb{1} = 0\;.\]
Why is this helpful? Well, \(\mathbb{1}\) is actually the eigenvector with smallest eigenvalue of the matrix \(\mathbf{D}^{-1}(\mathbf{D} - \mathbf{A})\).
So, the vector \(\mathbf{z}\) that we want must be the eigenvector with the second-smallest eigenvalue.
So, we will construct the matrix \(\mathbf{L} = \mathbf{D}^{-1}(\mathbf{D} - \mathbf{A})\), which is often called the (normalized) Laplacian matrix of the similarity matrix \(\mathbf{A}\). Next, we will find the eigenvector corresponding to its second-smallest eigenvalue, and call it z_eig. Then, we will plot the data again, using the sign of z_eig as the color.
L = np.linalg.inv(D) @ (D - A) # Laplacian matrix
eigenvalues, eigenvectors = np.linalg.eig(L)
idx = np.argsort(eigenvalues) # sort the eigenvalues
eigenvalues = eigenvalues[idx]
eigenvectors = eigenvectors[:, idx]
z_eig = eigenvectors[:, 1]
z_eigarray([ 0.09389207, 0.07736223, -0.06300698, -0.06253406, -0.07203744,
-0.06844687, -0.05944786, -0.06009116, 0.05131329, 0.03946165,
0.06620733, -0.06553515, -0.01103184, 0.05996065, 0.08757109,
0.07501904, 0.0572584 , -0.06303476, -0.07571484, -0.07031429,
0.0644712 , 0.03290825, 0.09343953, -0.06278897, -0.07955868,
0.04567633, -0.06045876, 0.06151979, 0.05555302, -0.06338615,
-0.06034508, 0.09371443, 0.07336238, 0.07147172, 0.05389553,
0.08160528, -0.07955868, 0.09261574, 0.08538788, -0.06813982,
0.07110439, -0.06321393, -0.06346373, -0.07993405, -0.07933222,
-0.06328915, -0.06307581, 0.06482837, 0.08710903, 0.01347952,
-0.06233862, -0.06056617, 0.09343953, 0.06090757, -0.0796757 ,
-0.07731147, 0.08189833, 0.03602595, 0.09290969, -0.06294241,
-0.0798901 , -0.07415366, 0.05089988, -0.06505416, 0.05811411,
-0.06897256, -0.0798901 , -0.07942743, -0.06238392, 0.09332248,
0.08361412, 0.09170838, 0.09355416, -0.0631895 , -0.0790602 ,
-0.05915303, 0.04468668, -0.06320357, 0.09280613, -0.06786225,
-0.05938268, -0.07278969, -0.07817252, 0.06725567, 0.06656592,
0.0848015 , 0.07147172, -0.06180046, -0.06269775, -0.06346513,
-0.05980403, 0.05089988, -0.0668405 , -0.06233862, 0.03602595,
0.03946165, 0.09261574, 0.08445433, -0.07597297, -0.06056617,
0.09287649, 0.08710903, 0.08223737, -0.04215372, 0.07189665,
0.06759655, -0.07304918, -0.06305594, 0.07848701, 0.05923704,
-0.0725521 , -0.07682128, -0.0626213 , 0.07571056, -0.06316259,
-0.07962072, -0.08018401, -0.05944786, 0.03602595, 0.07403544,
0.09199031, -0.07111864, 0.05346263, 0.09010294, 0.09363897,
-0.07783403, 0.08123258, -0.06128186, 0.09371443, 0.03602595,
-0.07861426, -0.05944786, -0.06294241, -0.0613566 , 0.0913628 ,
0.09310399, 0.06571268, 0.06171751, 0.06231661, 0.09411248,
0.04240836, 0.0902581 , -0.07880403, -0.06254634, 0.09405611,
-0.0789515 , -0.07440044, -0.07648554, -0.06338658, -0.06225021,
-0.06346373, -0.07861426, -0.0790602 , 0.04567633, 0.08845431,
-0.0798901 , 0.09378748, -0.06056617, -0.0789515 , -0.07817252,
0.07800947, 0.08257647, -0.06849123, -0.06180046, 0.0368132 ,
0.04567633, 0.06759655, -0.06254634, -0.05944786, -0.05906413,
0.09190167, -0.07670821, 0.05923704, 0.06554293, 0.0848015 ,
-0.06314009, -0.06319512, -0.07648554, -0.06307343, 0.09010294,
0.0572584 , -0.07809813, -0.07415366, 0.04338972, 0.05131329,
0.0499304 , -0.06306518, 0.05389553, 0.08189833, 0.08710903,
-0.06314009, 0.07800947, -0.06306518, 0.09054168, 0.06864681,
0.07501904, 0.04662749, -0.06443896, -0.06148957, -0.06422265])colors = ['red' if z < 0 else 'blue' for z in z_eig]
plt.scatter(X[:, 0], X[:, 1], c=colors)
plt.title('Data Clustering')
plt.show()
This looks essentially the same, but it took significantly less time!
Part G
We will synthesize our results from all the previous parts. In particular, we will write a function called spectral_clustering(X, epsilon) which takes in the input data X (in the same format as Part A) and the distance threshold epsilon and performs spectral clustering, returning an array of binary labels indicating whether data point i is in group 0 or group 1. We will demonstrate our function using the supplied data from the beginning of the problem.
Outline
Given data, we need to:
- Construct the similarity matrix.
- Construct the Laplacian matrix.
- Compute the eigenvector with second-smallest eigenvalue of the Laplacian matrix.
- Return labels based on this eigenvector.
def spectral_clustering(X, epsilon):
"""
Performs spectral clustering
Args:
X: original matrix containing coordinates for all data points
epsilon: the benchmark distance for classifying 'similarity'
Return:
labels: 0 if in cluster 0, 1 if in cluster 1
"""
distances = pairwise_distances(X)
similarity_matrix = np.where(distances <= epsilon, 1, 0)
np.fill_diagonal(similarity_matrix, 0)
D = np.diag(np.sum(similarity_matrix, axis=1))
L = np.linalg.inv(D) @ (D - similarity_matrix)
eigenvalues, eigenvectors = np.linalg.eig(L)
idx = np.argsort(eigenvalues)
eigenvalues = eigenvalues[idx]
eigenvectors = eigenvectors[:, idx]
z_eig = eigenvectors[:, 1]
labels = [0 if z < 0 else 1 for z in z_eig]
return labelslabels = spectral_clustering(X, 0.4)
plt.scatter(X[:, 0], X[:, 1], c=labels)
plt.title('Data Clustering')Text(0.5, 1.0, 'Data Clustering')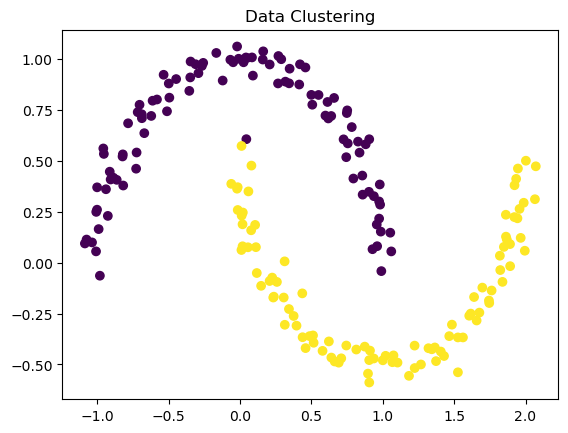
Part H
Let’s run one more experiment using our function, by generating a different data set using make_moons. What happens when we increase the noise? Will spectral clustering still find the two half-moon clusters? For these experiments, we might find it useful to increase n to 1000 or so – we can do this now, because of our fast algorithm!
n = 1000
X, y = datasets.make_moons(n_samples=n, shuffle=True, noise=0.12, random_state=None)
plt.scatter(X[:,0], X[:,1])
labels = spectral_clustering(X, 0.4)
plt.scatter(X[:, 0], X[:, 1], c=labels)
plt.title('Data Clustering')Text(0.5, 1.0, 'Data Clustering')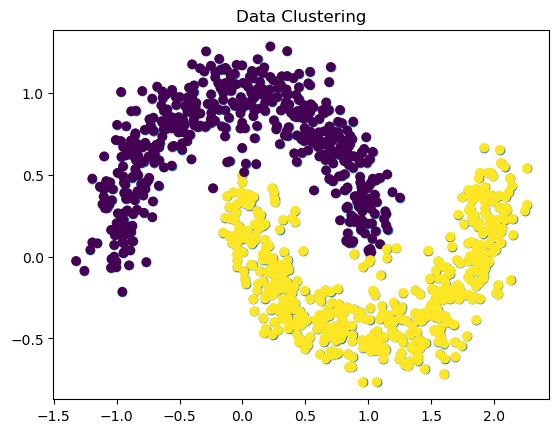
Part I
Now let’s try our spectral clustering function on another data set – the bull’s eye!
n = 1000
X, y = datasets.make_circles(n_samples=n, shuffle=True, noise=0.05, random_state=None, factor = 0.4)
plt.scatter(X[:,0], X[:,1])<matplotlib.collections.PathCollection at 0x7faed409fca0>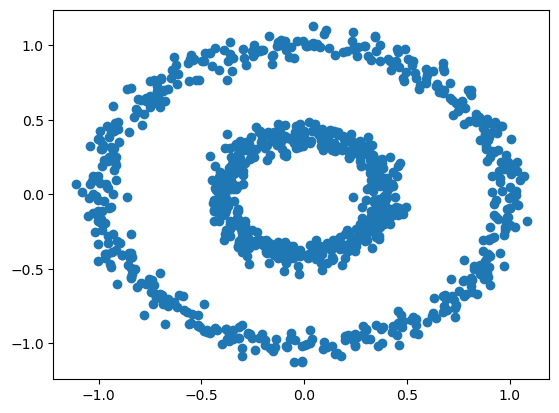
There are two concentric circles. As before k-means will not do well here at all.
km = KMeans(n_clusters = 2)
km.fit(X)
plt.scatter(X[:,0], X[:,1], c = km.predict(X))<matplotlib.collections.PathCollection at 0x7faecdc1a520>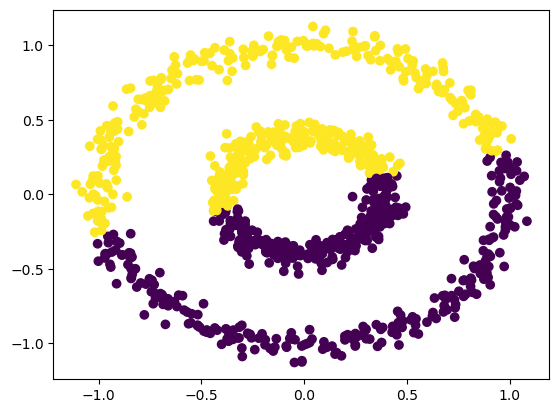
Can our function successfully separate the two circles? Some experimentation here with the value of epsilon is likely to be required.
labels = spectral_clustering(X, 0.4)
plt.scatter(X[:, 0], X[:, 1], c=labels)
plt.title('Data Clustering')Text(0.5, 1.0, 'Data Clustering')
Through experimentation, we find that an epsilon value of 0.4 is able to accurately cluster this data!